Proposition 1. - Let $f$ be a linear map of $E$ in an algebra $D$ over $A$ such that $f(x)^{2}=Q(x) . 1$ for all $x \in E$. There is one and only one homomorphism $\bar{f}$ of $C(Q)$ into $D$ such that $f=\bar{f} \circ \rho_{\tiny Q}$.
Proposition 1. - Soit $f$ une application linéaire de $E$ dans une algèbre $D$ sur $A$ telle que $f(x)^{2}=Q(x) . 1$ pour tout $x \in E$. Il existe un homomorphisme $\bar{f}$ et un seul de $C(Q)$ dans $D$ tel que $f=\bar{f} \circ \rho_{\tiny Q}$.
讨论:
以上列成公式即:
$$ f : E \to D $$
$$ \bar{f} : C(Q) \to D $$
$$ \exists! \ \bar{f}, f = \bar{f} \circ \rho_{\tiny Q} $$
译注:“un homomorphisme [name] et un seul de [src] dans [dst]” 的结构令人迷惑,此处一律按数学上的理解译为“one and only one homomorphism [name] of [src] into [dst]”,存在误译、漏译可能。
The uniqueness of $\bar{f}$ results from the fact that $C(Q)$ is generated by $\rho_{\tiny Q}(E)$. Let $h$ be the unique homomorphism of $T(E)$ into $D$ which extends $f$ ( $h$ is defined by $h\left(x_{1} \otimes \cdots \otimes x_{n}\right)=f\left(x_{1}\right) \ldots f\left(x_{n}\right)$ ). We have
$$
h(x \otimes x-Q(x) . 1) = \left(f(x)^{2}-Q(x)\right) . 1 = 0
$$
and then $h$ cancels on $I(Q)$ and defines the homomorphism $\bar{f}$ through the quotient.
L'unicité de $\bar{f}$ résulte de ce que $C(Q)$ est engendrée par $\rho_{\tiny Q}(E)$. Soit $h$ l'unique homomorphisme de $T(E)$ dans $D$ qui prolonge $f$ ( $h$ est défini par $h\left(x_{1} \otimes \cdots \otimes x_{n}\right)=f\left(x_{1}\right) \ldots f\left(x_{n}\right)$ ). On a
$$ h(x \otimes x-Q(x) . 1) = \left(f(x)^{2}-Q(x)\right) . 1 = 0 $$
et par suite $h$ s'annule sur $I(Q)$ et définit par passage au quotient l'homomorphisme $\bar{f}$ cherché.
讨论:
迄今为止的一系列映射,可以全部合成下面这张交换图:
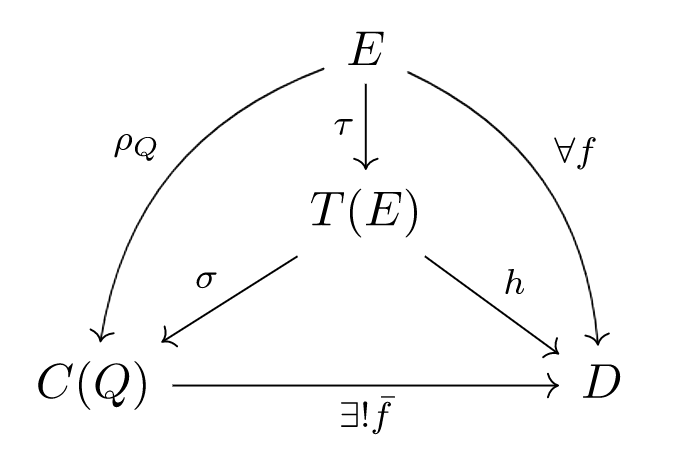
交换图源码(使用 https://tikzcd.yichuanshen.de/ 编辑,使用 https://upmath.me/ 渲染)见这里。
特别注意上图是在更完整的语境中,表达了Proposition 1里的
$$ \forall f, \exists ! \bar{f}, f = \bar{f} \circ \rho_{\tiny Q} $$
这个图的布局是经过专门推敲的。如果我们只是看泛性质本身,就是外围的弧边三角形,这个只涉及到最初的模$E$,最终的代数$D$,以及两者之间的$C(Q)$。弧边三角形里面的张量代数为其提供了构造性的“里子”。
译注:“par passage au ... cherché”的结构 令人迷惑,此处按数学上的理解译为“through ...”,存在误译、漏译的可能。
Prop. 1 shows that $C(Q)$ is a solution to a problem of universal (mapping) property ( Ens., chap. IV, § 3, $n^{\circ}$ 1 )
La prop. 1 exprime que $C(Q)$ est solution d'un problème d'application universelle ( Ens., chap. IV, § 3, $n^{\circ}$ 1 )
讨论:这里提到的Ens., chap. IV, § 3, $n^{\circ}$ 1 是 Théorie des ensembles 的 CHAPITRE IV. STRUCTURES 的 § 3. APPLICATIONS UNIVERSELLES 的 1. Ensembles et applications universels ,即在集合论中讲泛性质的章节。
Let us take in particular for $D$ the opposite algebra of $C(Q)$ and for $f$ the mapping $\rho$; prop. 1 implies that there is one and only one anti-automorphism $\beta$ of $C(Q)$ whose restriction to $\rho(E)$ is the identity; it is called the main anti-automorphism of C(Q). It is clear that $\beta^{2}=1$.
Prenons en particulier pour $D$ l'algèbre opposée de $C(Q)$ et pour $f$ l'application $\rho$; la prop. 1 entraine qu'il existe un antiautomorphisme $\beta$ et un seul de $C(Q)$ dont la restriction à $\rho(E)$ soit l'identité ; on l'appelle l'antiautomorphisme principal de C(Q). Il est clair que $\beta^{2}=1$.
讨论:反代数和反自同构安排在这里非常突兀,符号也没有明确区分开,会和最后的自同构一起讨论。
On the other hand, let $Q'$ be a quadratic form over an $A$ -module $E'$ and $f$ a linear map of $E$ into $E'$ such that $Q' \circ f=Q$. We have $\rho_{\tiny Q'}(f(x))^{2} = Q'(f(x)) . 1 = Q(x) . 1,$ and consequently there is one and only one homomorphism $C(f)$ of $C(Q)$ into $C(Q')$ such that $C(f) \circ \rho_{\tiny Q}=$ $\rho_{\tiny Q'} \circ f$.
D'autre part soient $Q'$ une forme quadratique sur un $A$ -module $E'$ et $f$ une application linéaire de $E$ dans $E'$ telle que $Q' \circ f=Q$. On a $\rho_{\tiny Q'}(f(x))^{2} = Q'(f(x)) . 1 = Q(x) . 1,$ et par suite il existe un homomorphisme $C(f)$ et un seul de $C(Q)$ dans $C(Q')$ tel que $C(f) \circ \rho_{\tiny Q}=$ $\rho_{\tiny Q'} \circ f$.
If $f$ is the identity, $C(f)$ is the identity ; if $Q''$ is a quadratic form over an $A$-module $E''$ and $g$ is a linear map of $E'$ into $E''$ such that $Q'' \circ g=Q'$, we have $C(g \circ f)=C(g) \circ C(f)$ . When $E'$ is a submodule of $E$ and $f$ is the canonical injection of $E'$ into E (so that $Q'$ is the restriction of $Q$ to $E'$ ), we say that $C(f)$ is the canonical homomorphism of $C(Q')$ into $C(Q)$.
Si $f$ est l'identité, $C(f)$ est l'identité ; si $Q''$ est une forme quadratique sur un $A$-module $E''$ et $g$ une application linéaire de $E'$ dans $E''$ telle que $Q'' \circ g=Q'$, on a $C(g \circ f)=C(g) \circ C(f)$. Lorsque $E'$ est un sous-module de $E$ et $f$ l'injection canonique de $E'$ dans E (de sorte que $Q'$ est la restriction de $Q$ à $E'$ ), on dit que $C(f)$ est l'homomorphisme canonique de $C(Q')$ dans $C(Q)$.
讨论:
以上两段,可以合成下面这张交换图:
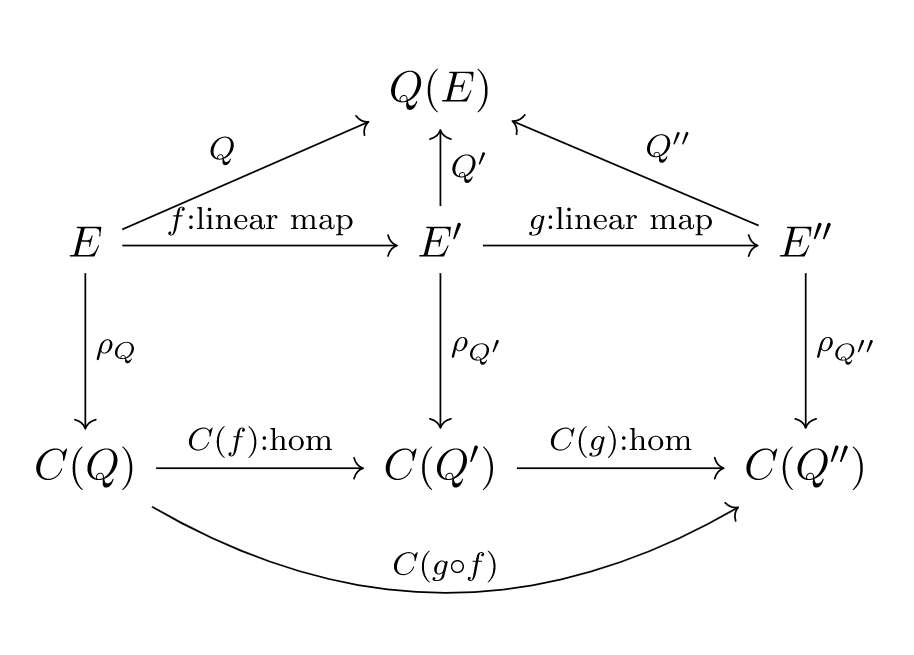
交换图源码(使用 https://tikzcd.yichuanshen.de/ 编辑,使用 https://upmath.me/ 渲染)见这里。
Let us take in particular $Q'=Q$ and for $f$ the mapping $x \to -x$; we see that there is an automorphism $\alpha$ and only one of $C(Q)$ such that $\alpha \circ \rho = -\rho$; it is called the main automorphism of $C(Q)$. It is clear that $\alpha^{2}=1$, and that the restriction of $\alpha$ to $C^{+}$ (resp. $C^{-}$ ) is the identity (resp. the mapping $u \to -u$ ).
Prenons en particulier $Q'=Q$ et pour $f$ l'application $x \to -x$; on voit qu'il existe un automorphisme $\alpha$ et un seul de $C(Q)$ tei que $\alpha \circ \rho=-\rho$; on l'appelle l'automorphisme principal de $C(Q)$. Il est clair que $\alpha^{2}=1,$ et que la restriction de $\alpha$ à $C^{+}$ (resp. $C^{-}$ ) est l'identité (resp. l'application $u \to -u$ ).
讨论:
这段自同构 $\alpha$ 和前面的反自同构 $\beta$ 的各个公式全部一起列出则是:
$$ f : Q \to_{l} Q' := u \mapsto -u$$
$$ Q = Q' $$
$$ \alpha : C(Q) \to C(Q) := q \mapsto f(q) $$
$$ \alpha \circ \rho = - \rho $$
$$ \alpha^{2} = 1 $$
$$ \alpha|_{C^+} := u \mapsto u $$
$$ \alpha|_{C^-} := u \mapsto -u $$
$$ \beta : C(Q) \to C^{op}(Q) $$
$$ \beta^{2} = 1 $$
$$ \beta|_{\rho(E)} := u \mapsto u $$
这里有一些符号需要解释下。
正常的数学文献中,$A \to B$ 和 $a \mapsto b$ 是并列的,只用逗号隔开。这里我化用了类似Lean的语法,$:$后的是映射(函数)的类型,即把什么集合(类型)映射到什么集合(类型),而$:=$ 则表示具体的定义,如何把某个元素如何地映射到另外一个集合。$\to_{l}$也是化用Lean的符号,表示线性映射。
Bourbaki没有使用$\mapsto$而一律使用了$\to$,容易混淆,所以这里区分了使用两者,但译文保持了原样。
$\alpha$ 是在原代数内部转悠,它应用两次会变成恒等映射,但应用一次,效果相当于取反。这是按性质或者说行为来定义它。这里的$f$是在帮助构造符合该性质的$\alpha$。
$\beta$ 是从代数到反代数(集合还是那个集合,乘法还是那个乘法,但相乘的顺序反过来),它应用两次也是在原代数上的恒等映射(反代数的反代数是原代数)。构造性地看,应用一次时,元素保持原样即可,只是映射前后生活在了相反的世界(代数)里,已经满足需要的性质。
这部分内容可以结合Arkadiusz Jadczyk英文版的Note中的1.2.2 Main involution $\alpha$ and main anti-involution $\tau$ 服用,文中的$\tau$就是$\beta$,$\lambda$就是$f$,$\pi$就是$\rho$,文中称之为involution(对合),个人理解,以此命名可能失之宽泛,因为involution有很多种,只要作用两次回到本身就可以,这里在讲的是具体的involutive (anti-)automorphism。
Proposition 2. - Let $A'$ be a commutative ring, $\varphi$ a homomorphism of $A$ into $A'$, $Q'$ the quadratic form over $E'= A' \otimes_{ A } E$ induced from $Q$ by extension of scalars (§ 3,$n^{\circ}$ 4, prop. 3 ). There is one and only one isomorphism $j$ of the algebra $A' \otimes_{ A } C ( Q )$ onto $C(Q')$ such that $j (1 \otimes \rho_{\tiny Q}(x) )=\rho_{\tiny Q'}(1 \otimes x)$ for all $x \in E$.
Proposition 2. - Soient $A'$ un anneau commutatif, $\varphi$ un homomorphisme de $A$ dans $A'$, $Q'$ la forme quadratique sur $E'= A' \otimes_{ A } E$ déduite de $Q$ par extension des scalaires (§ 3,$n^{\circ}$ 4, prop. 3 ). Il existe un isomorphisme $j$ et un seul de l'algèbre $A' \otimes_{ A } C ( Q )$ sur $C(Q')$ tel que $j (1 \otimes \rho_{\tiny Q}(x) )=\rho_{\tiny Q'}(1 \otimes x)$ pour tout $x \in E$.
It is sufficient to show that the algebra $C' = A' \otimes C(Q)$ and the mapping $1 \rho_{\tiny Q}$ of $E'$ into $C'$ form a solution to the same problem of universal (mapping) property as $C(Q')$ and $\rho_{\tiny Q'}$.
Now, let $D'$ be an algebra on $A'$ and $f'$ be a $A'$-linear application of $E'$ in $D'$ such that $f'(x')^2=Q'(x') .1$ for all $x' \in E'$. The mapping $g: x \to f'(1 \otimes x)$ of $E$ into $D'$ (considered as $A$-module thanks to the homomorphism $\varphi$ ) is A-linear and we have $g(x)^2=Q'(1 \otimes x). 1 = Q (x) .1$ for all $x \in E$. There is thus one and only one $A$-homomorphism $\bar{g}$ of $C(Q)$ into $D'$ such that $\bar{g}\left(\rho_{\tiny Q}(x)\right)=f'(1 \otimes x)$.
Therefore there is one and only one $A'$-homorphism $\bar{f'}$ of $C'$ into $D'$ such that $\bar{f'}\left(1 \otimes \rho_{\tiny Q }(x)\right)=f'(1 \otimes x)$ for all $x \in E$; by linearity it results that $\bar{f'}\left((1 \otimes \rho_{\tiny Q})(x')\right)=f'(x')$ for all $x' \in E'$. Q.E.D.
Il suffit de démontrer que l'algèbre $C' = A' \otimes C(Q)$ et l'application $1 \otimes \rho_{\tiny Q}$ de $E'$ dans $C'$ forment une solution du même problème d'application universelle que $C(Q')$ et $\rho_{\tiny Q'}$.
Or, soient $D'$ une algèbre sur $A'$ et $f'$ une application $A'$-linéaire de $E'$ dans $D'$ telle que $f'(x')^2=Q'(x') .1$ pour tout $x' \in E'$. L'application $g: x \to f'(1 \otimes x)$ de $E$ dans $D'$ (considéré comme $A$-module grâce à l'homomorphisme $\varphi$ ) est A-linéaire et on a $g(x)^2=Q'(1 \otimes x) . 1 = Q (x) .1$ pour tout $x \in E$. Il existe donc un $A$-homomorphisme $\bar{g}$ et un seul de $C(Q)$ dans $D'$ tel que $\bar{g}\left(\rho_{\tiny Q}(x)\right)=f'(1 \otimes x)$.
Par suite il existe un $A'$-homomorphisme $\bar{f'}$ et un seul de $C'$ dans $D'$ tel que $\bar{f'}\left(1 \otimes \rho_{\tiny Q }(x)\right)=f'(1 \otimes x)$ pour tout $x \in E$; par linéarité il en résulte que $\bar{f'}\left((1 \otimes \rho_{\tiny Q})(x')\right)=f'(x')$ pour tout $x' \in E'$. CQFD.
(持续更新,目前基本完成该节)
本文也发表于知乎:⧉